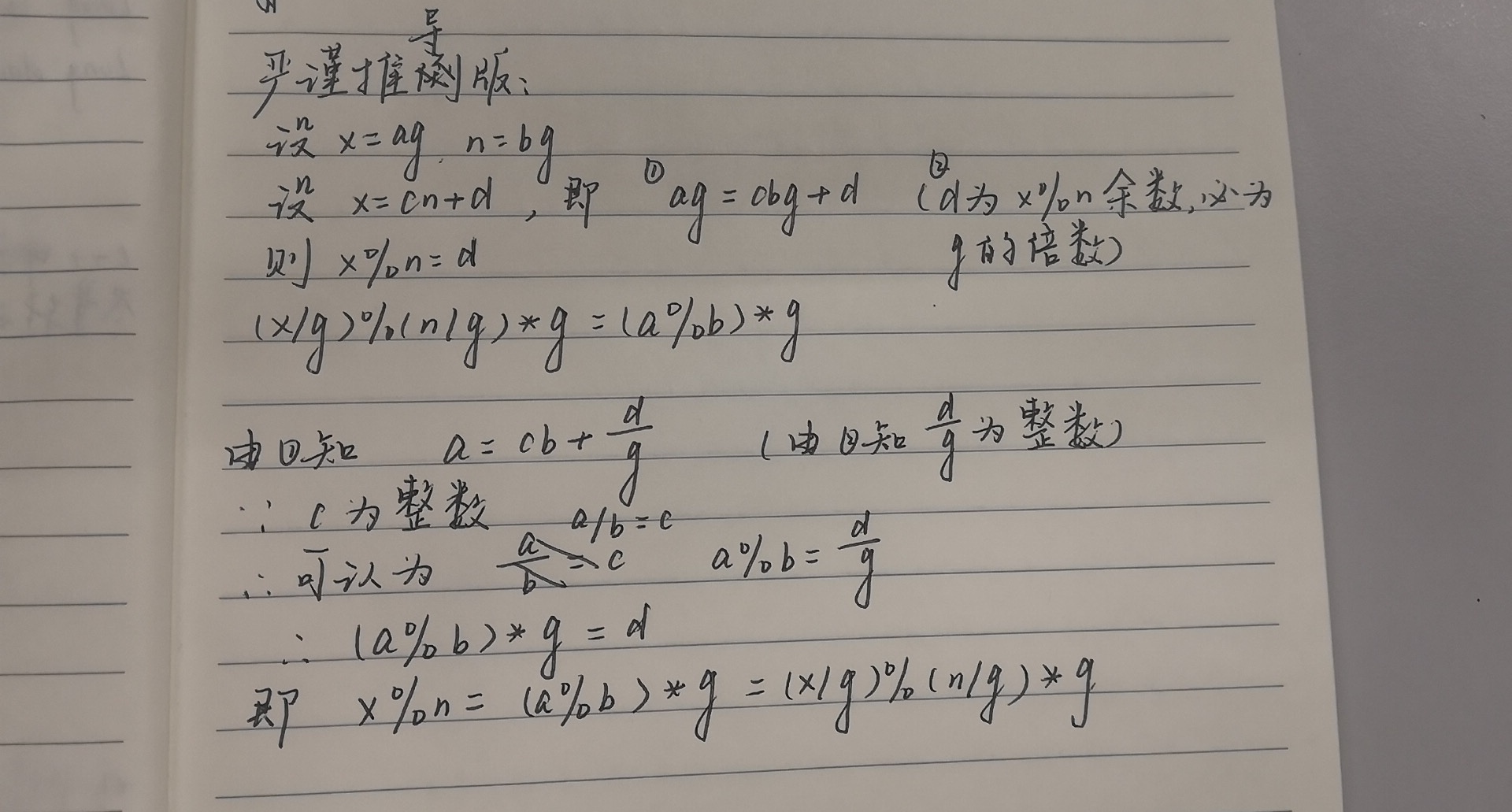面试流程

阿里的面试持续了1月左右，一共四轮，十分漫长。校招投递时间3月中旬，期间因为有考试麻烦了考官帮我延期3周，如果按照正常进度一周一面的话应该4月初结束。

一面（电话面）→笔试（在线测试）→二面（电话面）→三面（电话面）→四面（视频面）

一面

1小时，在笔试之前先面试是万万没想到的，可能因为是内推

问题：

1. 自我介绍

2. 描述TCP和UDP区别

3. 进程和线程区别

4. java内线程通信如何实现

5. 能讲一下数据库索引吗

6. 讲一下JVM虚拟机

7. 两道算法题，用阿里的伯乐系统在线做

   • 7-1 找一棵树中距离最远的两点距离
   • 7-2 给你n个数，表示一列并排的矩形，他们的宽度为1，高度为第i个数的值。问这堆矩形能形成的最大长方形面积

笔试

1小时，两道算法题

1. 忘记了，用到了栈
2. 一棵带边权的树，三个人每个人都有几个中意的点，在中意的点中居住的概率相同，三个人会选择距离和最近的点集合，问期望路程是多少。数据范围树的点数n<2e5，偏好酒店个数k<n, 时限3s。

二面

1. 自我介绍
2. 做过的项目介绍，会问简历中具体做过项目的细节，详细到你的思路，建模过程，实现过程中的难点
3. 有什么你在简历中没写的吗？会根据回答具体讨论，关于我的回答问题是
   • 3-1 产品经理需要有什么特质
   • 3-2 如果开发一款创新性的产品，例如发明微信，需要具备什么产品思维
4. JAVA的基本变量类型
5. TCP协议和IP协议的区别
6. 应用层有哪些协议

三面

1. 自我介绍
2. 职业规划
3. 数据库事务
4. 数据库的并发一致性问题，例如丢失修改，读脏数据，不可重复读，幻影读
5. 你本科最擅长的科目？根据回答会问相应问题，我回答了操作系统和数据结构，接下来用在线评测系统写代码
   • 5-1 实现生产者消费者
   • 5-2 每步可以走1 或 2 级台阶，有 n个台阶，问多少种走法

四面

1. 自我介绍
2. 根据简历项目，询问项目细节
3. 大学中做过的这些项目，印象最深刻的是，代表性的开发作品，锻炼了你什么
4. 解决一个问题，如何实现：淘宝中有很多商品，有些商品会被经常访问，就把他放到缓存中而不是数据库中，但是商品很多，如何决定把哪些商品放在缓存中？
5. 英文自我介绍
6. 英文3年职业规划

答案

答案是根据自己学的回答的，不是一定的标准答案，各种项目细节更是仅供参考描述。

写答案的主要原因是因为我在准备的过程中，参考了大量开源社区的整理，还有b站up主的视频，所以希望自己也能够帮到别人。

一面

1. 自我介绍

2. 描述TCP和UDP区别

   • 用户数据报协议 UDP（User Datagram Protocol）是无连接的，尽最大可能交付，没有拥塞控制，面向报文（对于应用程序传下来的报文不合并也不拆分，只是添加 UDP 首部），支持一对一、一对多、多对一和多对多的交互通信。
   • 传输控制协议 TCP（Transmission Control Protocol）是面向连接的，提供可靠交付，有流量控制，拥塞控制，提供全双工通信，面向字节流（把应用层传下来的报文看成字节流，把字节流组织成大小不等的数据块），每一条 TCP 连接只能是点对点的（一对一）。

3. 进程/线程/协程区别

   进程是资源管理单位，线程程序执行单位（这个执行程序是指kernel thread，才能真正的去执行程序，应用程序的thread和kernel thread 存在映射关系）为了提高routine切换成本比较低，协程是routine的一种实现

   Ⅰ 拥有资源

   进程是资源分配的基本单位，但是线程不拥有资源，线程可以访问隶属进程的资源。

   Ⅱ 调度

   线程是独立调度的基本单位，在同一进程中，线程的切换不会引起进程切换，从一个进程中的线程切换到另一个进程中的线程时，会引起进程切换。

   Ⅲ 系统开销

   由于创建或撤销进程时，系统都要为之分配或回收资源，如内存空间、I/O 设备等，所付出的开销远大于创建或撤销线程时的开销。类似地，在进行进程切换时，涉及当前执行进程 CPU 环境的保存及新调度进程 CPU 环境的设置，而线程切换时只需保存和设置少量寄存器内容，开销很小。

   Ⅳ 通信方面

   线程间可以通过直接读写同一进程中的数据进行通信，但是进程通信需要借助 IPC。

4. java内线程通信如何实现

   多种方法，详情见：https://redspider.gitbook.io/concurrent/di-yi-pian-ji-chu-pian/5

   利用锁与同步、等待通知机制、信号量、管道和其他方法等

5. 能讲一下数据库索引吗

   索引是加快了查询。

   数据库的索引实现是数据结构b+ 树。b+树非叶子结点不存储data，只存储索引，可以存放更多的索引叶子结点包含所有索引字段叶子结点用指针连接，提高区间访问的性能。

   innodb的索引是聚簇索引，主索引的叶子节点 data 域记录着完整的数据记录，这种索引方式被称为聚簇索引。因为无法把数据行存放在两个不同的地方，所以一个表只能有一个聚簇索引。辅助索引的叶子节点的 data 域记录着主键的值，因此在使用辅助索引进行查找时，需要先查找到主键值，然后再到主索引中进行查找。

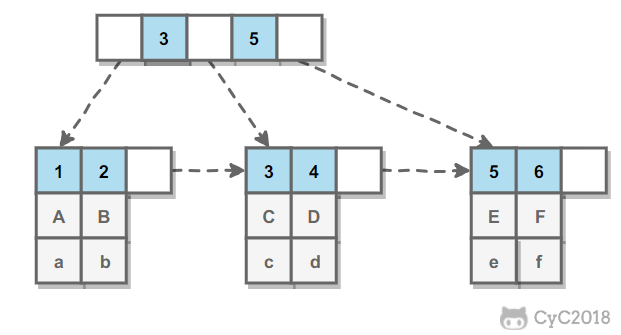
MyISAM是非聚簇索引，叶子节点上不存储数据。

关于联合索引，要注意建立索引时遵循左匹配原理。将区分度高的字段放在前面，区分度低的字段放后面。像性别、状态这种字段区分度就很低，我们一般放后面。

6. 讲一下JVM虚拟机

   java成为跨平台语言的关键

   所有线程共享的部分有：java堆，方法区

   每个线程私有的是：pc寄存器，java虚拟机栈，本地方法栈

   各部分的功能详情见：

   链接

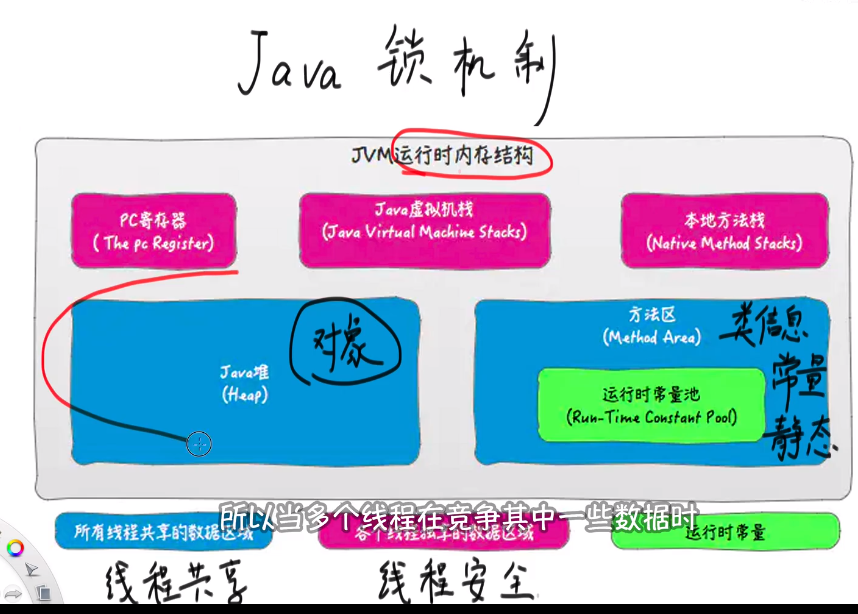
7. 两道算法题，用阿里的伯乐系统在线做

   • 7-1 找一棵树中距离最远的两点距离

     dfs。

     方法一：对每个结点，维护子节点的最长链和次长链，最远点的距离就是对某个结点的最长链+次长链长度

     方法二：实际上是求树的直径。第一遍dfs找到最远点，然后把这个结点作为根节点再跑一次dfs找到最远点。两次找到的点都是直径的端点

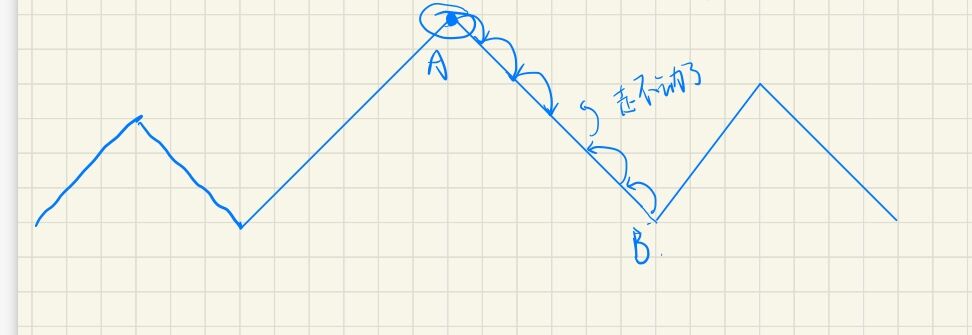
   • 7-2 给你n个数，表示一列并排的矩形，他们的宽度为1，高度为第i个数的值。问这堆矩形能形成的最大长方形面积

     栈

     暴力想法：我们肯定对每个高度，都尽量找它向左和向右最远到哪

     可以用高度递增的栈维护上面的边界，记录结点的位置和高度，栈中保证结点高度是非递减的，这样每当一个新节点加入时，栈内的点如果高度小于等于它就压进去，大于它的话就把栈顶弹(hi,xi)掉。弹掉时维护答案，它的高度*（当前要加入栈数位置-它栈下一个数的位置）

笔试

1小时，两道算法题

1. 简单题，忘记了，用到了栈

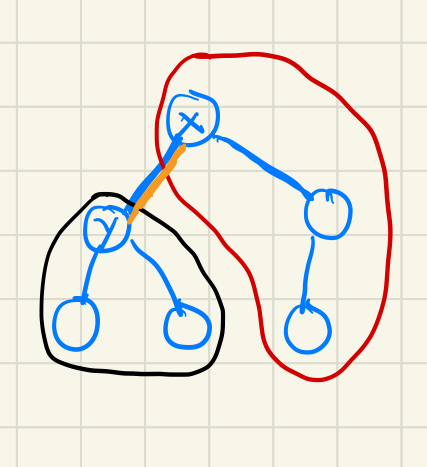
2. 一棵带边权的树，三个人每个人都有几个中意的点，在中意的点中居住的概率相同，三个人会选择距离和最近的点集合，问期望路程是多少。数据范围树的点数n<2e5，偏好酒店个数k<n, 时限3s。

   一条边对答案的贡献是他左右两边的不同人的方案数， 因为这条边必须被经过才能在这些选点方式中将三个点连通 且三个点连通的最短情况下每条路径上的边只会被经过一次

   核心代码

   1 2 3 4 5 6

   tmp=cou[v][1]*(num[2]-cou[v][2])*(num[3]-cou[v][3]); tmp+=cou[v][2]*(num[1]-cou[v][1])*(num[3]-cou[v][3]); tmp+=cou[v][3]*(num[2]-cou[v][2])*(num[1]-cou[v][1]); tmp+=cou[v][2]*cou[v][3]*(num[1]-cou[v][1]); tmp+=cou[v][1]*cou[v][3]*(num[2]-cou[v][2]); tmp+=cou[v][1]*cou[v][2]*(num[3]-cou[v][3]);

二面

1. 自我介绍

2. 做过的项目介绍，会问简历中具体做过项目的细节，详细到你的思路，建模过程，实现过程中的难点

3. 有什么你在简历中没写的吗？会根据回答具体讨论，关于我的回答问题是

   • 3-1 产品经理需要有什么特质
   • 3-2 如果开发一款创新性的产品，例如发明微信，需要具备什么产品思维

4. JAVA的基本变量类型

   • byte/8
   • char/16
   • short/16
   • int/32
   • float/32
   • long/64
   • double/64
   • boolean/~

5. TCP协议和IP协议的区别

   tcp是运输层协议，IP是网络层协议。

   运输层是解决进程之间基于网络的通信问题，是端到端通信。

   网络层是解决分组在多个网络上传输的问题

6. 应用层有哪些协议

   https、ftp、smtp等

三面

1. 自我介绍

2. 职业规划

3. 数据库事务

   事务指的是满足 ACID 特性的一组操作，可以通过 Commit 提交一个事务，也可以使用 Rollback 进行回滚。

   • 1.数据库事务可以包含一个或多个数据库操作,但这些操作构成一个逻辑上的整体。
   • 2.构成逻辑整体的这些数据库操作,要么全部执行成功,要么全部不执行。
   • 3.构成事务的所有操作,要么全都对数据库产生影响,要么全都不产生影响,即不管事务是否执行成功,数据库总能保持一致性状态。
   • 4.以上即使在数据库出现故障以及并发事务存在的情况下依然成立。

   例如：

   1 2 3 4

   >BEGIN TRANSACTION >A账户减少100元 >B账户增加100元 >COMMIT

   事务使系统能够更方便的进行故障恢复以及并发控制,从而保证数据库状态的一致性。

4. 数据库的并发一致性问题，例如丢失修改，读脏数据，不可重复读，幻影读

5. 你本科最擅长的科目？根据回答会问相应问题，我回答了操作系统和数据结构，接下来用在线评测系统写代码

   • 5-1 实现生产者消费者。是多线程通信的例子

   • 链接

     哎。当时没写出来，好难啊。先鸽了，以后补上！

   • 5-2 每步可以走1 或 2 级台阶，有 n个台阶，问多少种走法。要求写注释，排版好看点。。。

     递归

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

     //问题：每步可以走1 或 2 级台阶，有 n个台阶，问多少种走法 #include<iostream> #include<cstdio> using namespace std; const int maxn=10000; //总方案数 int tot = 0; //方案记录数组 int v[maxn],num; void dfs(int cou){ if(cou == n){ //输出方案 //总方案数+1 tot++; printf("现在是第%d 种方案，走法是：",tot); for(int i = 1;i <= num;i++)printf("%d ",v[i]); cout<<endl; return ; } //不能构成方案，返回 if(cou > n)return; //这一步走一级台阶 v[++num]=1; dfs(cou+1); //回溯 num--; //这一步走两级台阶 v[++num]=2; dfs(cou+2); num--; } int main(){ dfs(0); //输出总方案数 cout<<tot<<endl; }

四面

1. 自我介绍
2. 根据简历项目，询问项目细节

化学建筑项目。

光能转化模型

1. 太阳能电池最佳倾角
2. 向光材料接受率分析
3. 编程原理

问了模型设计的难点，考虑将建模与AI结合，创新点，学到了什么，建模过程

1. 大学中做过的这些项目，印象最深刻的是，代表性的开发作品，锻炼了你什么

产品经理

微北洋，轻北洋。设计的特点，两者区别。

产品的创新点！突出特点

定位

1. 解决一个问题，如何实现：淘宝中有很多商品，有些商品会被经常访问，就把他放到缓存中而不是数据库中，但是商品很多，如何决定把哪些商品放在缓存中？

   实际是缓存淘汰算法

   1.LRU 最近最久未使用

   LRU 近最久未使用的页面换出。

   第一种实现方式直接用链表。 当一个页面被访问时，将这个页面移到链表表头。但是每次都要遍历链表，代价较高。

   第二种实现方式hashmap+链表。查询数据是否在链表中用hashmap。当需要插入新的数据项的时候，如果新数据项在链表中存在（命中），则把该节点移到链表头部，如果不存在，则新建一个节点，放到链表头部，若缓存满了，则把链表最后一个节点删除即可。在访问数据的时候，如果数据项在链表中存在，则把该节点移到链表头部，否则返回-1。这样一来在链表尾部的节点就是最近最久未访问的数据项。

   2. NRU 最近未使用

   两个标记R/M。R标记被访问，M标记被修改。R位会定时清零。页面分为4类：

   R=0, M=0

   R=0, M=1

   R=1, M=0

   R=1, M=1

   发生缺页中断，随机从编号最小的非空类中选一个页面换出。

   NRU优先换出已被修改的脏页面（R=0,M=1)，而不是被频繁使用的干净页面（R=1,M=0)

2. 英文自我介绍

3. 英文3年职业规划

感受

第一面是最懵逼的，因为是第一次投实习，第一次面试，根本不知道还有面经这种东西存在。没有准备，以为凭着本科所学直接上，实际上证明了——我本科什么都没有学的深入，或者说没学到能记住细节，几乎所有被问的问题都是对这个问题在哪堂课见过有个印象，但是答不上来，万幸的是面试官见我基础太差就直接开始考算法题。果然只有大学打过的acm印在了脑子里。基础太差又薄弱，也没有项目支撑。

还有阿里的面试官非常准时，一般跟你约好的时间会准时出现，后来我就在约好的时间提前半小时提前准备了。

第一面结束后很受挫，开始认真准备面试。大体分为三步：

1.基础知识学习。

2.看视频，理解技术细节。

3.刷面经，对着题目回答。

基础知识复习参考：

http://www.cyc2018.xyz/#%E7%AE%97%E6%B3%95

细节讲解，有很多不错的b站教程：

https://www.bilibili.com/video/BV1c4411d7jb?p=44&t=661

https://www.bilibili.com/video/BV14z4y1d7Wa?t=912

https://www.bilibili.com/video/BV1aE41117sk?p=8&t=1023

https://www.bilibili.com/video/BV1Wr4y1A7DS

面经：牛客网，很多面经。

https://www.nowcoder.com/discuss/620617?channel=-1&source_id=discuss_terminal_discuss_history_nctrack&ncTraceId=0de4c2957e304ce1b6b8fb84384fbd59.956.16182236949048605

复习了1周左右，难受的是感觉东西越学越多，java不咋会写，还要学spring框架，操作系统的算法看了就忘。期间收藏了不少好课，十足的好课，可惜我大学前两年学基础时没有干脆自己看网课学这些。例如湖科的b站计网课，还有清华向勇老师的操作系统，可惜当年不知道，想今年有机会把这些看完。

第二、三、四面都意识流偏多，考官很喜欢聊科研中的细节，因为2年产品经理，每个考官都有和我聊到产品，还有4场面试中，3场都有算法题，感谢大学加入了天外天和acm，大一不经意做出的选择悄然间改变了发展的轨迹。

参加实习面试的还有一件影响就是它让我开始回顾自己。一是，接受自己很菜的事实，从高中起身边就已经有了让我仰慕的学术idol，都是在自己领域做的闪闪发光的人，他们的很多博客，记录都有影响到我追着脚步一点点前进；二是，感谢和珍重曾经做的每一次选择，大一刚入学的时候真的很迷茫，那时候我甚至一口气在百团大战报过10个社团，我大概属于对自己的未来规划有方向，却对具体实施不太清醒的人，大二的时候才明白，重点在于做减法而不是做加法，做好一件事足矣，只留下了天外天和acm，回想9.1日开学喻老师把我们召集起来开始布置acm训练，和9.31日坐在天外天的面试官前什么都不懂的我，肯定不知道悄然改变了3年后的自己。

更希望在阿里做开发可以学到很多东西，希望明年想起来发现这一年学会了更多的东西！

好吧其实这一阵子焦虑的很。

hahah

A. Perfectly Imperfect Array

题解

只要任意一个数不是平方数就可以

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

#include<bits/stdc++.h>
using namespace std;
int const maxn=2e5+10;
int main(){

	int t,n,a,v;
	cin>>t;
	while(t--){
		scanf("%d",&n);
		bool flag=false;
		for(int i=1;i<=n;i++){
			scanf("%d",&a);
			v=sqrt(a);
			if(v*v!=a)flag=true;
		}
		if(flag)printf("YES\n");
		else printf("NO\n");
	}	
	return 0;
}

B . AND 0, Sum Big

题意：

给你N和K, 问有多少长度为n的数组满足：

• 所有元素在[0,\(2^k-1\) ]范围内
• 所有元素AND值为0
• 所有元素之和尽可能大

题解：

快速幂：二进制k位，只要每一位有一个0就能满足条件2，为了满足条件3每一位只能在数组中的一个数中为0，所以每一位的选择有n个数，答案为\(n^k\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

#include<bits/stdc++.h>
using namespace std;
long long p=1e9+7;
long long n,k,t;
long long  pow_fast(long long  a,long long  b,long long  mod){
	long long  num=1%mod;
	for(;b;b>>=1,a=a*a%mod)
	  if(b&1)num=num*a%mod;
	return num;
}
int main(){
	cin>>t;
	while(t--){
		scanf("%lld%lld",&n,&k);
		long long ans=pow_fast(n,k,p);
		printf("%lld\n",ans);
	}	
	return 0;
}

C . Product 1 Modulo N

题意：

给定n，问[1,n-1]范围内，最多可以取多少数，使其乘积取模n为1

数据范围：

\[\left( 2 \leq n \leq 10^{5}\right)\]

题解：

首先知道一个结论：如果a，b的最大公约数g=gcd(a,b)不为1，则a%b大于1，因为a%b的余数一定是g的倍数。

（1） a%b = (a/g) % (b/g) * g

所以只能选与n互质的数，他们的乘积取余n的结果x也与n互质，x就在刚刚所取的数中，只要把x删掉就行了

证明1： a%b = (a/g) % (b/g) * g

证明:2：与b互质的数乘积取余b的余数与b互质

设 \(a_1,a_2,a_3..a_m\) 与b互质 z=a_1a_2a_3 z=n*b+p g=gcd(n,p) n=cg , p=dg z=gcb+dg=g(cb+d) 则 g是 z 的因子，如果g ≠ 1,则n与 z不互质，与题设矛盾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include<bits/stdc++.h>
using namespace std;
vector<int> v;
int gcd(int a,int b)//最大公约数，辗转相除 
{
	return b?gcd(b,a%b):a;
}
int main(){
	int n;
	scanf("%d",&n);
	v.push_back(1);
	long long tmp=1;
	for (long long i=2;i<n;i++){
		if (gcd(i,n)==1){//只能选与n互质的数
			v.push_back(i);
			tmp=(1ll*tmp*i)%n;
		} 
	}
	if (tmp==1ll) cout<<v.size()<<endl;
	else cout<<v.size()-1<<endl;
	for (long long i=0;i<v.size();i++){
		if (v[i]==tmp&&tmp!=1) continue;
		cout<<v[i]<<" ";//余数>1时，把余数删
	}
	cout<<endl;
}

网上看到的另一种不错证明，原文链接

不能选与n不互质的数, 因为选了之后%n一定不为1,因为gcd(乘积,n)!=1. 证明: 设gcd(p,n)=z,则p=xz,n=yz, 设选的其他数乘积为q, 则pq%n=1,设pq=kn+1, 那么qxz=kyz+1, (qx-ky)z=1, 当且仅当z=1时式子才有可能成立, 而gcd=z>1,因此式子不可能成立, 所以如果选择了gcd!=1的数,一定不满足条件.

因此只能选与n互质的数, 设s为所有与n互质的数的积对n取模的结果, 如果s=1,那么这些数全部可以选择, 如果s!=1,此时s一定与n互质,因此s也在这些数中, 那么选除了s的其他数就行了

D. Cut and Stick

题意：

给出长度为n的序列a，q个询问，每次询问[l,r]区间。

问至少把区间内的数重新组合成几段，才能满足每段众数的次数不超过 \(\left \lceil len \right \rceil\) , len为区间长度

数据范围：

\(\left( 1 \leq n,q \leq 3*10^{5}\right)\)

\(a_{1}, a_{2, \ldots,} a_{n}\left(1 \leq a_{i} \leq n\right)\)

\((1 \leq l \leq r \leq n)\)

题解：

1. 如果初始区间众数个数< \(\left \lceil len \right \rceil\) , 则不用拆，答案为1。否则就要拆，关于每段如何拆分。

偶→奇+奇 ，可容纳数增加1；奇→偶+奇，可容纳数不变。于是每次就是尽量拆偶数，变化如下

初始偶→奇+奇→偶+奇+奇→奇+奇+奇+奇→偶+奇++奇+奇+奇...

初始奇→偶+奇→奇+奇+奇→偶+奇++奇+奇...

实际上就是初始为偶数多了一步，后面跟奇数一样拆法。每多1个，段数+2。

2. 莫队求区间众数，时间复杂度n*sqrt(n)。开一个数组num记录每个数的个数，数组cou[x]记录数量为x的数有几个。

每次区间增加时，增加这个数的个数，维护cou。还有判断增加后是否变成区间众数

区间变小时，减少这个数的个数，维护cou。看当前众数个数值的cou是否变为0，如果变为0说明当前数为唯一众数，众数个数应该-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

#include<bits/stdc++.h>
using namespace std;
// #define debug(x,i) cout<<"haha"<<i<<' '<<x<<endl;
int const MAXN = 3e5+7;
int a[MAXN],unit,n,m,nowmax,cnt[MAXN],ans[MAXN],num[MAXN];
struct query1{
    int L,R,id;
}qu[MAXN];
bool cmp(query1 a,query1 b){
    if(a.L/unit == b.L/unit)    //相同块，对R排序
        return a.R < b.R;
    else return a.L/unit <b.L/unit; //不同块，对块排序
}
void mo_add(int x){
	cnt[num[a[x]]]--;
	num[a[x]]++;
	cnt[num[a[x]]]++;
	if(num[a[x]]>nowmax)nowmax=num[a[x]];
}
void mo_del(int x){
	cnt[num[a[x]]]--;
	num[a[x]]--;
	cnt[num[a[x]]]++;
	if(cnt[nowmax]==0)nowmax--;
}
void work(){
    int L = 1,R = 0;
    for(int i=0;i<m;i++){
        while(R < qu[i].R){
            R++;
            mo_add(R);
        }
        while(R > qu[i].R){
            mo_del(R);
            R--;
        }
        while(L < qu[i].L){
            mo_del(L);
            L++;
        }
        while(L > qu[i].L){
            L--;
            mo_add(L);
        }
        // debug(nowmax,1);
     	if(nowmax<=ceil((R-L+1)/2.0))ans[qu[i].id]=1;
     	else{//奇偶不同拆法
     		int z=1,len=R-L+1,u=nowmax-ceil((R-L+1)/2.0);
     		if(len%2==0){z++;u--;}
     		while(u){
     			z+=2;u--;
     		}
     		ans[qu[i].id]=z;
     	}   
    }
}

int main(){
   scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    unit=sqrt(n);
    for(int i=0;i<m;i++){  //读入查询
        scanf("%d%d",&qu[i].L,&qu[i].R);
        qu[i].id = i;
    }
    sort(qu,qu+m,cmp);
    work();
    for(int i=0;i<m;i++){
        printf("%d\n",ans[i]);
    }
    return 0;
}

比赛时：

想到了莫队，但是当莫队区间变小时卡住了，忘记了只要再维护一个众数的个数有多少就行了。

A . Split it!

题解

从开头和结尾向中间找最长的相同长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include<bits/stdc++.h>
using namespace std;
const int maxn=110;
int t,n,k;
char s[maxn];
bool work(){
	if(n<=k*2)return 0;
	int l=-1,r=n;
	while(l+1<r-1 && s[l+1]==s[r-1]){
		l++;r--;
	}
	if(l+1>=k)return 1;
	return 0;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&k);
		scanf("%s",s);

		if(work())printf("YES\n");
		else printf("NO\n");
	}
	return 0;
}

B . Max and Mex

题解：

1. 如果mex为n，则每次向后插入mex，k次之后不同的值为n+k个
2. 如果mex不为n，则每次插入的都是同一个值，如果这个值出现过，k次之后不同的值为n个；如果没出现过，k次之后不同的值为n+1个

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int t;
long long n,k,a[maxn];
long long getmex(){
	int v=0;
	for(int i=1;i<=n;i++,v++){
		if(v!=a[i])return v;
	}
	return v;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%lld%lld",&n,&k);
		for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
		sort(a+1,a+1+n);
		long long mex=getmex();
		if(mex==n)printf("%lld\n",n+k);
		else{
			if(k==0){
				printf("%lld\n",n);
				continue;
			}
			long long  mid = ceil((mex+a[n])/2.0);
			if(a[lower_bound(a+1,a+n+1,mid)-a]==mid)printf("%lld\n",n);
			else printf("%lld\n",n+1);
		}
	}
	return 0;
}

C . Diamond Miner

题意：

n个矿工在y轴上，n个矿在x轴上，一个人挖一个，花费的力气是点之间的欧几里得距离。问如何分配使得总花费最小

数据范围：

\[\left( 1 \leq n \leq 10^{5}\right)\]

题解：

绝对值相同的点是等价的，直接用|x||y|来代替x,y

会发现两个数组排序后，顺着配的值最小，即小的和小的，大的和大的。

证明方法是排序不等式：

定理：设 \(0<a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n}, 0<b_{1} \leqslant b_{2} \leqslant \cdots\leqslant b_{n}\) 为两组实数, \(c_{1}, c_{2}, \cdots, c_{n}\) 为 \(b_{1}, b_{2}, \cdots, b_{n}\) 的任一排列，则有 \[ \begin{array}{l} \sqrt{a_{1}^{2}+b_{n}^{2}}+\sqrt{a_{2}^{2}+b_{n-1}^{2}}+\cdots+\sqrt{a_{\mathrm{n}}^{2}+b_{1}^{2}} \\ \geqslant \sqrt{a_{1}^{2}+c_{1}^{2}}+\sqrt{a_{2}^{2}+c_{2}^{2}}+\cdots+\sqrt{a_{n}^{2}+c_{n}^{2}} \\ \geqslant \sqrt{a_{1}^{2}+b_{1}^{2}}+\sqrt{a_{2}^{2}+b_{2}^{2}}+\cdots+\sqrt{a_{n}^{2}+b_{n}^{2}} \end{array} \] 其中全相等 \(\Leftrightarrow a_{1}=a_{2}=\cdots=a_{n}\) 或 \(b_{1}=b_{2}=\cdots=b_{n} .\)

证明方法，把两个排列相减呗

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int t, n;
long long a[maxn],b[maxn];
double dis;
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		dis=0;
		int tot=n*2,tot1=0,tot2=0;
		long long x,y;
		for(int i=1;i<=tot;i++){
			scanf("%lld%lld",&x,&y);
			if(x==0)a[++tot1]=abs(y);
			else b[++tot2]=abs(x);
		}
		sort(a+1,a+1+n);
		sort(b+1,b+1+n);
		for(int i=1;i<=n;i++){
			dis+=sqrt(a[i]*a[i]+b[i]*b[i]);
		}
		printf("%.10lf\n",dis);
	}
	return 0;
}

补充下关于 \(\sum_{i=1}^{n} \sqrt{a_{i}^{2}+b_{i}^{2}}\left(a_{i}, b_{i} \in \mathbf{R}\right)\) 的不等式定理

柯西不等式： 设 \(a_{1}, a_{2}, \cdots, a_{n} ; b_{1}, b_{2}, \cdots, b_{n}\) 为实数, \(n \in \mathbf{N}\),\(n \geqslant 2,\) 则 \(\sqrt{a_{1}^{2}+b_{1}^{2}}+\sqrt{a_{2}^{2}+b_{2}^{2}}+\cdots+\sqrt{a_{n}^{2}+b_{n}^{2}} \geqslant\) \(\sqrt{\left(a_{1}+a_{2}+\cdots+a_{n}\right)^{2}+\left(b_{1}+b_{2}+\cdots+b_{n}\right)^{2}}\) 其中等号成立 \(\Leftrightarrow\) 存在非负实数 \(\lambda\) 及 \(\mu(\lambda, \mu\) 不同时为0)\(,\) 使得 \(\lambda a_{i}=\mu b_{i}(i=1,2, \cdots, n) .\)

D . Let's Go Hiking

先丢一个队友题解链接：https://blog.csdn.net/weixin_43877657/article/details/114933752

题意：

给出一个长度为n的排列，a先选一个位置，然后b再选一个位置，两人每次都可以向周围移动1位，满足移动后的位置a的值比原来小，b的值比原来小。两人都会采取最优策略，问初始时a选位置能赢的个数

数据范围：

\[\left( 2 \leq n \leq 10^{5}\right)\]

题解：

1. 首先a要选在坡顶，坡腰b能把它堵死
2. a要选在最大峰的坡顶，否则b能选能大峰的坡地开始走
3. 这个破必须长度为奇数，a会与b对着走，奇数才能在相会时让b无法走
4. 不能有其他坡和这个坡长度相同，也就会说这个破不仅最大还唯一，否则b可以走那个

画个示意图，注意上面4点坑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

a,b,k=map(int,input().split())
if(k==0):
    s='1'*b+'0'*a
    print("Yes\n"+s+"\n"+s)
elif(a==0):
    print("No");
else:
    if a+b-2<k or b==1:
        print("No")
    else:
        s='1'*(b-1)+'0'*(a-1)
        print("Yes")
        print(s[:a+b-k-1]+'1'+s[a+b-k-1:]+'0')
        print(s[:a+b-k-1]+'0'+s[a+b-k-1:]+'1')
        

比赛时：

那个破不能超过一个没想到qwq

常见写代码错误

1. long long 数据非常大的时候！ 再大用 int128
2. 多组数据清空！记得把栈、set也清空

哈哈哈哈

ICPC PACIFIC NORTHWEST REGION 原题链接

A Radio Prize

题意：

一颗树，每个点点权ti，边权wi。输出n行，每行代表第x个点，它到所有点的 两点权和*路径 之和

\[ ans_x=\sum_{v=1}^{n} (t_x+t_v)d_{x,v}\]

数据范围

1<=k<=n<=200000

题解：

树形dp/树分治。想了两种转移方式

planA（简单）：

\(ans_x\)由两部分构成，根节点 * 路径和+子节点 * 对应路径的和

设该树的根节点为 \(x,\) \[ \begin{array}{l} a_{x}=\sum_{v=1}^{n} d_{x, v} \\ b_{x}=\sum_{v=1}^{n} t_{v} d_{x, v} \end{array}\\ ans_x=t_xa_x+b_x \] 结点y与x相邻，设以y为根节点的子树大小为\(tot_y\)，子树点权值和为\(sum_y\)，总点数为n，总点权和为SUM，则从x转到子节点y的方程为：

\[\begin{array}{l} a_{y}=a_{x}+w_{xy}(n-2tot_y) \\ b_{x}=b_{x}+w_{xy}(SUM-2sum_y) \end{array}\\\]

转移解释：

从x到y，橘色边w造成的影响有，黑色部分的点路径都减去w，红色部分的点路径都加上w

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10;
int tot,head[maxn],n,m,val[maxn],tson[maxn],SUM;
long long aa[maxn],bb[maxn],sum[maxn],ans[maxn];
struct edge{
    int v,nxt;
    long long w;
}e[maxn<<1];
void build(int x,int y,int z){
    e[++tot].v=y;
    e[tot].nxt=head[x];
    e[tot].w=z;
    head[x]=tot; 
}
void TreeSplitDfs1(int x,int f){
    tson[x]=1;
    sum[x]=val[x];
    for(int i=head[x];i;i=e[i].nxt){
        int v=e[i].v;
        if(v==f)continue;
        TreeSplitDfs1(v,x);
        tson[x]+=tson[v];
        sum[x]+=sum[v];
        aa[1]+=e[i].w*tson[v];
        bb[1]+=e[i].w*sum[v];
    }
}
void TreeSplitDfs2(int x,int f){
    for(int i=head[x];i;i=e[i].nxt){
        int v=e[i].v;
        if(v==f)continue;
        aa[v]=aa[x]+e[i].w*(n-2*tson[v]);
        bb[v]=bb[x]+e[i].w*(SUM-2*sum[v]);
        ans[v]=val[v]*aa[v]+bb[v];
        TreeSplitDfs2(v,x);
    }
}
int main(){
    
    scanf("%d",&n);
    tot=0;
    memset(head,0,sizeof(int)*(n+5));
    int a,b,c;
    for(int i=1;i<=n;i++){
        scanf("%d",&val[i]);
        SUM += val[i];
    }
    for(int i=1;i<n;i++){
        scanf("%d%d%d",&a,&b,&c);
        build(a,b,c);
        build(b,a,c);
    }
    TreeSplitDfs1(1,0);
    ans[1]=val[1]*aa[1]+bb[1];
    TreeSplitDfs2(1,0);
    for(int i=1;i<=n;i++)printf("%lld\n",ans[i]);//注意 long long 


    return 0;
}

planB（复杂）:

\(ans_x\)由两部分构成 ： 所有边 * 子树结点和 + 边 * 子节点个数 * 根节点权。算了转移太难写了，维护的东西还麻烦。。。不写了

B Perfect Flush

题意：给出n个数的序列，数字范围为1~k，找k个数都包含的最小子序列，保证有解。

数据范围

1<=k<=n<=200000

题解：贪心。我们肯定希望越小的元素放在前面越好，大的元素如果还有就把它尽量往后放，用栈来维护。

如果如果一个数在栈内，不管这个数。一个栈如果当前数小于栈顶，栈顶元素在后面还有的话，就把栈顶弹出，重复到不再弹栈，把这个数压进去。

结果为栈中的序列。

注意：在栈中的元素不要再用它来做弹栈操作了。因为它出现在前面更优。如下图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

#include <iostream>
#include <stack>
using namespace std;
int const maxn=200005;
int n,k,ans[maxn],tot,cou[maxn],a[maxn],g[maxn];
stack<int>s;
int main(){
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		cou[a[i]]++;
	}
	tot=0;
	for(int i=1;i<=n;i++){
		if(g[a[i]]>0)continue;//如果是栈里已经有的，说明在前面更有意义，不要用它来弹出栈里的东西了
		if(!s.empty()){
			int u=s.top();
			while(cou[u]>0&&u>=a[i]){
				s.pop();
				g[u]--;
				if(s.empty())break;
				u=s.top();
			}	
		}
		s.push(a[i]);
		g[a[i]]++;
		cou[a[i]]--;
	}
	for(int i=k;i>0;i--){
		ans[i]=s.top();
		s.pop();
	}
	for(int i=1;i<k;i++){
		printf("%d ",ans[i]);
	}
	printf("%d\n",ans[k]);
	return 0;
}
/*
9 8
4 3 5 8 3 1 6 7 2*/

C Coloring Contention

题意：

对图的边染色，使从1到n的路径中颜色变化最少的路径颜色变化最多。（最大化最小值）

数据范围：

2<=n<=1e5 1 <= m <= 1e5

题解：

bfs 染色 ，交替染色，当前点的出点中没染色的染为相反颜色，边跟出点同色。

答案：顺便用bfs找最短路，如果最短路为k，那最大变k-1次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10;
int tot,head[maxn],n,m,val[maxn],dis[maxn];
bool vis[maxn];
struct edge{
    int v,nxt;
}e[maxn<<1];
void build(int x,int y){
    e[++tot].v=y;
    e[tot].nxt=head[x];
    head[x]=tot;
}
queue<int>q;
int main(){

    scanf("%d%d",&n,&m);
    tot=0;
    memset(head,0,sizeof(int)*(n+5));
    int a,b;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&a,&b);
        build(a,b);
        build(b,a);
    }
    q.push(1);
    int x;
    vis[1]=1;
    dis[1]=0;
    while(!q.empty()){
        x=q.front();q.pop();
        for(int i=head[x];i;i=e[i].nxt){
            int v=e[i].v;
            if(vis[v])continue;
            vis[v]=1;
            q.push(v);
            dis[v]=dis[x]+1;
            if(v==n)break;
        }
    }
    printf("%d\n",dis[n]-1);
    return 0;
}

D Dividing by Two

题意：

问从A变到B的最小操作数，可以执行两个操作： 1.把A/2，只有A是奇数时可以 2.把A+1

数据范围：

​ \[ 1 \leq a,b \leq10^{9}\]

题解：

暴力。a<b输出b-a,a>b就一直除或加变到小于

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10;
long long a,b;
int main(){
	scanf("%lld%lld",&a,&b);
	if(a<b)printf("%lld\n",b-a);
	else{
		long long ans=0;
		while(a>b){
			if(a%2==0)a/=2;
			else a++;
			ans++;
		}
		printf("%lld\n",ans+(b-a));
	}
	return 0;

}

E Rainbow Strings

题意：

给出字符串s，求所有字母不相同的子序列数量（空字符串也算） 答案取模11 092 019.

数据范围：

​ \[ 1 \leq len(s) \leq10^{5}\]

题解：

记录每个字母的数量num[i], \[ans= \prod_{i=a}^{z} num[i]+1\]

反正每个字母最多选一次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10,mod=11092019;
char s[maxn];
long long  cou[600];
int main(){
	scanf("%s",s);
	int len=strlen(s);
	for(int i=0;i<len;i++){
		cou[(int)s[i]]++;
	}
	long long ans=1;
	for(int i='a';i<='z';i++)ans=(ans*(cou[i]+1))%mod;
	printf("%lld\n",ans);
	
	return 0;

}

F Carny Magician

求n个数的排列，满足：第k小的，有m个数在原位（pi=i）

G Glow, Little Pixel, Glow

？？qwq没太看明白

H Pivoting Points

？？qwq？？qwq

I Error Correction

题意：

n个字符串(字符串中没有重复的字母，隐含字符串最长26)，找到一个最大子集，使其中两两字符串x,y不能通过交换1对字母（不需要相邻）成为对方

输出最大子集大小

数据范围：

​ \[ 1 \leq N \leq 500\]

题解：

二分图最大独立集。

预处理：哪些字符串可以相互到达能暴力对比求出，把能相互转化到的字符串连一条边，问题变为找一般图的最大独立集。或者：把不能到达的字符串之间连边，问题变为找一般图的最大完全子图。

独立集：任意两点之间没有连边。

完全图：任意两点之间右边。

一般图的独立集或完全图时间复杂度过高，转化为二分图。

J Interstellar Travel

给定Ti ,si ,ai最大化

\[\sum_{1}^{n}\max \left(0, T_{i}-s_{i} \cdot \operatorname{dist}\left(a_{i}, a\right)\right) \]

dist(ai,a) 是ai到a最小转动的弧度

K Computer Cache

有n个字节的内存初始为0，下标从1到n

有m条数据 xi

询问q次三种操作之一：

1. 1 i p 把第i条数据放到内存p 到p+len(xi)-1位置,保证操作有效不会溢出
2. 2 p 询问内存p位置是什么数
3. i l r 把xi中l到r位置数字都加1，对256取模

L Carry Cam Failure

定义一种新运算 加法没有进位，乘法运算中也无进位 给一个N，求最小的a满足a⊗a=N ，如果没有输出-1

M Maze Connect

？？qwq

A

一个环，分成k端，每段的值是所有数|起来，总值是所有端&起来。输出最大值

B

一张有自环、重边的有向图，边的耗时都为1

前k个点有生产机器，每个点j在 x*k+j 时刻产生一个产品(x>=0)

一条路在某刻只有一个产品，路口不限产品数，

问前k个点可以留下那几台机器，使满足所有产品都能被运到第n个点

C

题意

给出n个区间[ s_i , t_i ]，问这些区间总覆盖数字多少个

数据范围

n<100, si,ti<365

题解

前缀和维护，然后暴力看一下那些数字有值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

#include<bits/stdc++.h>
using namespace std;
int const maxn=400;
int qwq[maxn],sum[maxn];
int main(){
	int n;
	scanf("%d",&n);
	int a,b;
	for(int i=1;i<=n;i++){
		scanf("%d%d",&a,&b);
		qwq[a]+=1,qwq[b+1]-=1;
	}
	int ans=0;
	for(int i=1;i<=365;i++){
		sum[i]=sum[i-1]+qwq[i];
		if(sum[i]>0)ans++;
	}
	printf("%d\n",ans);
	return 0;
}

D

题意：

给出一张无向图（可能还有多个连通块），如果1个点感染病毒，他可以感染它邻居的邻居，你可以在一些点之间加边。问最少加几条边可以使最初感染一个点后扩散到所有点都被感染。

题解：

一个连通块内，如果含有一个奇环（环由奇数个点构成），就能感染整个连通块。

所以只要判断图中有几个连通块，有没有一个连通块中含有奇环。先把所有连通块联通，没有奇环的话多花1条边建立奇环。

判断奇环：暴力黑白染色

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

#include<bits/stdc++.h>
using namespace std;
int const maxn=5e5+10;
int tot,head[maxn],n,m,val[maxn],f[maxn],se[maxn];
bool vis[maxn];
struct edge{
    int v,nxt;
}e[maxn<<1];
void build(int x,int y){
    e[++tot].v=y;
    e[tot].nxt=head[x];
    head[x]=tot;
}
void prime(){
    for(int i=1;i<=n;i++)            //初始化并查集，代表元素是自己； 
    f[i]=i;
}

int find(int x){
    if(f[x]==x)return f[x];
    f[x]=find(f[x]);                      //查询同时路径压缩； 
    return f[x];
}

void merge(int x,int y){
    int f1=find(x),f2=find(y);
    f[f1]=f2;
} 
bool you=1;
void ranse(int x){
    vis[x]=1;
    if(you==0)return ;
    for(int i=head[x];i;i=e[i].nxt){
        int v=e[i].v;
        if(vis[v]){
            if(se[x]==se[v]){
                you=0;return ;
            }
        }
        else se[v]=1-se[x];
    }
    for(int i=head[x];i;i=e[i].nxt){
        int v=e[i].v;
        if(!vis[v])ranse(v);
    }
}
int main(){
    
    scanf("%d%d",&n,&m);
    prime();
    tot=0;
    memset(head,0,sizeof(int)*(n+5));
    int a,b;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&a,&b);
        build(a,b);
        build(b,a);
        merge(a,b);
    }
    
    int ans=0;
    for(int i=1;i<=n;i++){
        if(find(i)==i){
            ans++;
            ranse(i);
        }
    }
    printf("%d\n", ans-1+you);
    return 0;
}

E

给n个点，求选3个点，最大的三角形面积。

题解：

凸包+旋转卡壳

F

给定字符串s，可以改变最多k次s中的字符，如果改动后的字符串中出现连着三个或以上的相同字符，这一串字符会变为 * ，问最多让几个字符最后变为 * 。

G

题意

问某个数的非质因子有多少个

题解：

预处理欧拉筛法质因子分解（记录每个数第一次被那个数筛掉），假设一个数x的m个质因子次数分别为 a1,a2....am

ans= (a1+1)*(a2+1)...(am+1)-m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include<bits/stdc++.h>
using namespace std;
int const maxn=2000010;
int prime[maxn],s[maxn];
int cntprime = 0;
bool flag[maxn];
void euler(){
	for (int i = 2; i < maxn; i++){
	    if (!flag[i]) prime[++cntprime] = i;
	    for (int j = 1; j <= cntprime && prime[j] * i < maxn; j++){
	        flag[i * prime[j]] = true;
	        s[i*prime[j]]=prime[j];//存每个数的最小质因子
	        if (i % prime[j] == 0)
	            break;
	    }
	}
}
int main(){
	int t;
	scanf("%d",&t);
	int a,b;
	euler();
	for(int i=1;i<=t;i++){
		scanf("%d",&a);
		if(flag[a]==0){
			printf("1\n");
			continue;
		}
		int ans=1,cou=0,v=sqrt(a);
		// for(int j=1;j<=cntprime;j++){
		// 	if(prime[j]>v)break;

		// 	if(a%prime[j]==0){
		// 		// cout<<prime[j]<<endl;
		// 		int tot=0;
		// 		while(a%prime[j]==0){
		// 			tot++;
		// 			a/=prime[j];
		// 		}
		// 		ans*=(tot+1);
		// 		cou++;
		// 	}
		// }一开始直接暴力求质因子，tle了
		while(s[a]){//一直除最小质因子
			cou++;
			int tot=0,v=s[a];
			while(a%v==0){
				tot++;
				a/=v;
			}
			ans*=(tot+1);
		}
		if(a>1){ans*=2;cou++;}
		printf("%d\n",ans-cou);
	}
	
	return 0;
}

比赛:

别暴力质因数分解啊！！

H

给出初始字母s，每个字母有一个替换规则，进行k次替换。

m次询问，问替换完后某个位置的数是多少

l

在r*c的矩形中，选n次子矩形，这些子矩形都至少含有k个相同的格子。问有多少种方案，某一次选的格子不同即为一种不同方案。

J

K

L

在序列中找字典序最小的A B A B

哈哈哈

哈哈哈

问题：

一开始参考了几个网站，使用如下命令安装新的渲染引擎

npm uninstall hexo-renderer-marked –save npm install hexo-renderer-kramed –save

结果报错：

pandoc exited with code 9: pandoc: Unknown extension: smart_

原因：

参考网站：https://theme-next.js.org/docs/third-party-services/math-equations

next主题与 hexo-katex 插件冲突

解决办法：

换用 hexo-renderer-pandoc

1. 确保电脑内安装有最新版pandoc,版本不低于2。pandoc安装地址： https://www.pandoc.org/installing.html

   用 pandoc --version 查看电脑内pandoc版本

2. 卸载旧渲染器，下载 hexo-renderer-pandoc

npm un hexo-renderer-marked npm i hexo-renderer-pandoc

3. 更改主题配置文件 next/_config.yml 中如下部分

math: ...

every_page: false

mathjax: enable: true

every_page：true渲染每一页，false只会渲染头文件中mathjax: true 的文章

4. 测试

hexo clean

hexo g

hexo s

A . Three swimmers

题解

找p离a,b,c倍数最近的那个

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include<bits/stdc++.h>
using namespace std;
long long mod=1000000007;
long long ans,a,b,c,p;
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%lld%lld%lld%lld",&p,&a,&b,&c);
		ans=a-((p-1)%a+1);
		ans=min(ans,b-((p-1)%b+1));
		ans=min(ans,c-((p-1)%c+1));
		printf("%lld\n",ans);
	}
	return 0;
}

B . Card Deck

题解：

使值大的尽量在底下，每次取都取到当前剩的最大的一个

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include<bits/stdc++.h>
using namespace std;
long long mod=1000000007;
int const maxn=1e5+7;
typedef long long ll;
ll n,a[maxn],ne[maxn],ans;
int p[maxn];
int main(){
	int t;
	scanf("%d",&t);
	while(t--){

		scanf("%lld",&n);
		for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
		p[1]=1;
		for(int i=2;i<=n;i++){
			if(a[i]>a[p[i-1]])p[i]=i;
			else p[i]=p[i-1];
		}
		int qwq=n,tot=0;
		while(qwq>0){
			for(int i=p[qwq];i<=qwq;i++){
				ne[++tot]=a[i];
			}
			qwq=p[qwq]-1;
		}
		for(int i=1;i<n;i++){
			printf("%lld ",ne[i]);
		}
		printf("%lld\n",ne[n]);
	}
	return 0;
}

C . Maximum width

题意：

给出长度为n的字符串s，长度为m的字符串t

求构造一个长度m递增数列p， \[1 \leq p_{1} \le p_{2} \le \ldots \le p_{m} \leq n\] 满足 \(s_{pi} = t_i\) , p的宽度定义为 \(\max _{1 \leq i<m}\left(p_{i+1}-p_{i}\right)\)，即最大的相 邻的差

保证一定能构造出一组p，求p的最大宽度

数据范围：

\[\left( 2 \leq m \leq n \leq 2 \cdot 10^{5}\right)\]

题解：

使相邻的pi 和 pi+1 差最大，就要使pi取尽量靠左的s中的位置，pi+1取尽量靠右的s中的位置

为了维护p递增，先从左向右扫一遍维护出最小值pl，再从右向左扫一遍维护出最大值pr，再扫一遍枚举分界点 \[ans=max \left( pr[i+1]-pl[i] \right)\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include<bits/stdc++.h>
using namespace std;
int const maxn2=2e5+7;
int l[maxn2],r[maxn2],n,m;
string s1,s2;
int main(){
	scanf("%d%d",&n,&m);
	cin>>s1>>s2;
	
	int ans=-maxn2;
	int qwq=0;
	for(int j=0;j<m;j++){
		while(s1[qwq]!=s2[j])qwq++;
		l[j]=qwq;
		qwq++;
	}
	qwq=n-1;
	for(int j=m-1;j>=0;j--){
		while(s1[qwq]!=s2[j])qwq--;
		r[j]=qwq;
		qwq--;
	}
	for(int i=0;i<m-1;i++){
		ans=max(r[i+1]-l[i],ans);
	}
	printf("%d\n",ans);

	return 0;
}

比赛时：

我居然忘记了p是递增的，直接求了pi+1在s中的最右减去，pi在s中的最左。。。。

假题意代师。。。

D . Genius's Gambit

题意：

构造两个含a个0，b个1的二进制数x,y(x>=y)，两者之差的二进制数含k个1。

数据范围：\[(0≤a, 1≤b; 0≤k≤a+b≤2⋅10^5)\]

题解：

两个错位的1和0，中间全部相同，能减出一组1，例如：

\[11110000-\\01110001=\\01111111\]

利用这个规律可以构造出所有a+b-2>=k （k,a>=1,b>=2）的情况

特判：只有0个0的，或者1个1（因为不允许前导零），不能构造出1。k=0时一定能满足。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

a,b,k=map(int,input().split())
if(k==0):
    s='1'*b+'0'*a
    print("Yes\n"+s+"\n"+s)
elif(a==0):
    print("No");
else:
    if a+b-2<k or b==1:
        print("No")
    else:
        s='1'*(b-1)+'0'*(a-1)
        print("Yes")
        print(s[:a+b-k-1]+'1'+s[a+b-k-1:]+'0')
        print(s[:a+b-k-1]+'0'+s[a+b-k-1:]+'1')
        

比赛时：

没有想到只要错位中间一样就可以了。。以为要分0和1讨论

没有想到k=0一定满足

没有注意到1个1，或者0个0都不能构造出来。

比完赛简直是面向样例编程。。。

E . Almost Fault-Tolerant Database

题意：

n个m长的数组，

构造一个数组，满足它改变最多两个值可以得到任意一个给出的n个数组

不存在输出no

数据范围：

\[(2 \leq n ; 1 \leq m ; n \cdot m \leq 250000)\]

题解：

网上看到的。枚举构造

假设以第一个数组为模板，跟后面的作对比

1. 有数组跟它>4个不同，则无解

2. 所有的<=两个不同，则直接输出第一个数组

3. 有4个不同，则第一个数组至少要改2位，枚举改的两位和改的值

4. 有3个不同，如果有一位所有3个的都有且为同一个值，则改这一位，否则等同于第三种情况，枚举改哪两位哪个值，