2019 ICPC Pacific Northwest Region Conteste

发表于 2021-03-12 更新于 2021-03-13 分类于算法阅读次数：

ICPC PACIFIC NORTHWEST REGION 原题链接

A Radio Prize

题意：

一颗树，每个点点权ti，边权wi。输出n行，每行代表第x个点，它到所有点的两点权和*路径之和

\[ ans_x=\sum_{v=1}^{n} (t_x+t_v)d_{x,v}\]

数据范围

1<=k<=n<=200000

题解：

树形dp/树分治。想了两种转移方式

planA（简单）：

\(ans_x\)由两部分构成，根节点 * 路径和+子节点 * 对应路径的和

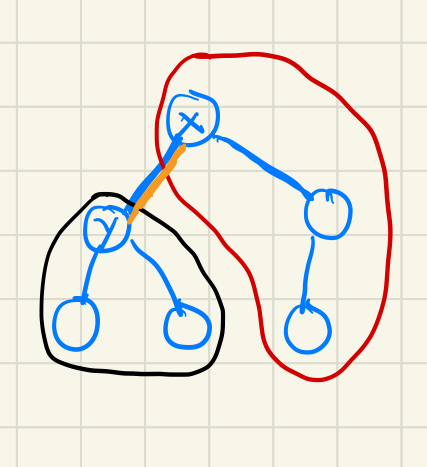
设该树的根节点为 \(x,\) \[ \begin{array}{l} a_{x}=\sum_{v=1}^{n} d_{x, v} \\ b_{x}=\sum_{v=1}^{n} t_{v} d_{x, v} \end{array}\\ ans_x=t_xa_x+b_x \] 结点y与x相邻，设以y为根节点的子树大小为\(tot_y\)，子树点权值和为\(sum_y\)，总点数为n，总点权和为SUM，则从x转到子节点y的方程为：

\[\begin{array}{l} a_{y}=a_{x}+w_{xy}(n-2tot_y) \\ b_{x}=b_{x}+w_{xy}(SUM-2sum_y) \end{array}\\\]

转移解释：

从x到y，橘色边w造成的影响有，黑色部分的点路径都减去w，红色部分的点路径都加上w

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10;
int tot,head[maxn],n,m,val[maxn],tson[maxn],SUM;
long long aa[maxn],bb[maxn],sum[maxn],ans[maxn];
struct edge{
    int v,nxt;
    long long w;
}e[maxn<<1];
void build(int x,int y,int z){
    e[++tot].v=y;
    e[tot].nxt=head[x];
    e[tot].w=z;
    head[x]=tot; 
}
void TreeSplitDfs1(int x,int f){
    tson[x]=1;
    sum[x]=val[x];
    for(int i=head[x];i;i=e[i].nxt){
        int v=e[i].v;
        if(v==f)continue;
        TreeSplitDfs1(v,x);
        tson[x]+=tson[v];
        sum[x]+=sum[v];
        aa[1]+=e[i].w*tson[v];
        bb[1]+=e[i].w*sum[v];
    }
}
void TreeSplitDfs2(int x,int f){
    for(int i=head[x];i;i=e[i].nxt){
        int v=e[i].v;
        if(v==f)continue;
        aa[v]=aa[x]+e[i].w*(n-2*tson[v]);
        bb[v]=bb[x]+e[i].w*(SUM-2*sum[v]);
        ans[v]=val[v]*aa[v]+bb[v];
        TreeSplitDfs2(v,x);
    }
}
int main(){
    
    scanf("%d",&n);
    tot=0;
    memset(head,0,sizeof(int)*(n+5));
    int a,b,c;
    for(int i=1;i<=n;i++){
        scanf("%d",&val[i]);
        SUM += val[i];
    }
    for(int i=1;i<n;i++){
        scanf("%d%d%d",&a,&b,&c);
        build(a,b,c);
        build(b,a,c);
    }
    TreeSplitDfs1(1,0);
    ans[1]=val[1]*aa[1]+bb[1];
    TreeSplitDfs2(1,0);
    for(int i=1;i<=n;i++)printf("%lld\n",ans[i]);//注意 long long 


    return 0;
}

planB（复杂）:

\(ans_x\)由两部分构成：所有边 * 子树结点和 + 边 * 子节点个数 * 根节点权。算了转移太难写了，维护的东西还麻烦。。。不写了

B Perfect Flush

题意：给出n个数的序列，数字范围为1~k，找k个数都包含的最小子序列，保证有解。

数据范围

1<=k<=n<=200000

题解：贪心。我们肯定希望越小的元素放在前面越好，大的元素如果还有就把它尽量往后放，用栈来维护。

如果如果一个数在栈内，不管这个数。一个栈如果当前数小于栈顶，栈顶元素在后面还有的话，就把栈顶弹出，重复到不再弹栈，把这个数压进去。

结果为栈中的序列。

注意：在栈中的元素不要再用它来做弹栈操作了。因为它出现在前面更优。如下图：

#include <iostream>
#include <stack>
using namespace std;
int const maxn=200005;
int n,k,ans[maxn],tot,cou[maxn],a[maxn],g[maxn];
stack<int>s;
int main(){
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		cou[a[i]]++;
	}
	tot=0;
	for(int i=1;i<=n;i++){
		if(g[a[i]]>0)continue;//如果是栈里已经有的，说明在前面更有意义，不要用它来弹出栈里的东西了
		if(!s.empty()){
			int u=s.top();
			while(cou[u]>0&&u>=a[i]){
				s.pop();
				g[u]--;
				if(s.empty())break;
				u=s.top();
			}	
		}
		s.push(a[i]);
		g[a[i]]++;
		cou[a[i]]--;
	}
	for(int i=k;i>0;i--){
		ans[i]=s.top();
		s.pop();
	}
	for(int i=1;i<k;i++){
		printf("%d ",ans[i]);
	}
	printf("%d\n",ans[k]);
	return 0;
}
/*
9 8
4 3 5 8 3 1 6 7 2*/

C Coloring Contention

题意：

对图的边染色，使从1到n的路径中颜色变化最少的路径颜色变化最多。（最大化最小值）

数据范围：

2<=n<=1e5 1 <= m <= 1e5

题解：

bfs 染色，交替染色，当前点的出点中没染色的染为相反颜色，边跟出点同色。

答案：顺便用bfs找最短路，如果最短路为k，那最大变k-1次。

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10;
int tot,head[maxn],n,m,val[maxn],dis[maxn];
bool vis[maxn];
struct edge{
    int v,nxt;
}e[maxn<<1];
void build(int x,int y){
    e[++tot].v=y;
    e[tot].nxt=head[x];
    head[x]=tot;
}
queue<int>q;
int main(){

    scanf("%d%d",&n,&m);
    tot=0;
    memset(head,0,sizeof(int)*(n+5));
    int a,b;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&a,&b);
        build(a,b);
        build(b,a);
    }
    q.push(1);
    int x;
    vis[1]=1;
    dis[1]=0;
    while(!q.empty()){
        x=q.front();q.pop();
        for(int i=head[x];i;i=e[i].nxt){
            int v=e[i].v;
            if(vis[v])continue;
            vis[v]=1;
            q.push(v);
            dis[v]=dis[x]+1;
            if(v==n)break;
        }
    }
    printf("%d\n",dis[n]-1);
    return 0;
}

D Dividing by Two

题意：

问从A变到B的最小操作数，可以执行两个操作： 1.把A/2，只有A是奇数时可以 2.把A+1

数据范围：

\[ 1 \leq a,b \leq10^{9}\]

题解：

暴力。a<b输出b-a,a>b就一直除或加变到小于

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10;
long long a,b;
int main(){
	scanf("%lld%lld",&a,&b);
	if(a<b)printf("%lld\n",b-a);
	else{
		long long ans=0;
		while(a>b){
			if(a%2==0)a/=2;
			else a++;
			ans++;
		}
		printf("%lld\n",ans+(b-a));
	}
	return 0;

}

E Rainbow Strings

题意：

给出字符串s，求所有字母不相同的子序列数量（空字符串也算）答案取模11 092 019.

数据范围：

\[ 1 \leq len(s) \leq10^{5}\]

题解：

记录每个字母的数量num[i], \[ans= \prod_{i=a}^{z} num[i]+1\]

反正每个字母最多选一次

#include<bits/stdc++.h>
using namespace std;
int const maxn=1e5+10,mod=11092019;
char s[maxn];
long long  cou[600];
int main(){
	scanf("%s",s);
	int len=strlen(s);
	for(int i=0;i<len;i++){
		cou[(int)s[i]]++;
	}
	long long ans=1;
	for(int i='a';i<='z';i++)ans=(ans*(cou[i]+1))%mod;
	printf("%lld\n",ans);
	
	return 0;

}

F Carny Magician

求n个数的排列，满足：第k小的，有m个数在原位（pi=i）

G Glow, Little Pixel, Glow

？？qwq没太看明白

H Pivoting Points

？？qwq？？qwq

I Error Correction

题意：

n个字符串(字符串中没有重复的字母，隐含字符串最长26)，找到一个最大子集，使其中两两字符串x,y不能通过交换1对字母（不需要相邻）成为对方

输出最大子集大小

数据范围：

\[ 1 \leq N \leq 500\]

题解：

二分图最大独立集。

预处理：哪些字符串可以相互到达能暴力对比求出，把能相互转化到的字符串连一条边，问题变为找一般图的最大独立集。或者：把不能到达的字符串之间连边，问题变为找一般图的最大完全子图。

独立集：任意两点之间没有连边。

完全图：任意两点之间右边。

一般图的独立集或完全图时间复杂度过高，转化为二分图。

J Interstellar Travel

给定Ti ,si ,ai最大化

\[\sum_{1}^{n}\max \left(0, T_{i}-s_{i} \cdot \operatorname{dist}\left(a_{i}, a\right)\right) \]

dist(ai,a) 是ai到a最小转动的弧度

K Computer Cache

有n个字节的内存初始为0，下标从1到n

有m条数据 xi

询问q次三种操作之一：

1 i p 把第i条数据放到内存p 到p+len(xi)-1位置,保证操作有效不会溢出
2 p 询问内存p位置是什么数
i l r 把xi中l到r位置数字都加1，对256取模

L Carry Cam Failure

定义一种新运算加法没有进位，乘法运算中也无进位给一个N，求最小的a满足a⊗a=N ，如果没有输出-1

M Maze Connect

？？qwq