[CF1496] Codeforces Round #706 (Div. 2)

发表于 2021-03-21 分类于算法阅读次数：

A . Split it!

题解

从开头和结尾向中间找最长的相同长度

#include<bits/stdc++.h>
using namespace std;
const int maxn=110;
int t,n,k;
char s[maxn];
bool work(){
	if(n<=k*2)return 0;
	int l=-1,r=n;
	while(l+1<r-1 && s[l+1]==s[r-1]){
		l++;r--;
	}
	if(l+1>=k)return 1;
	return 0;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&k);
		scanf("%s",s);

		if(work())printf("YES\n");
		else printf("NO\n");
	}
	return 0;
}

B . Max and Mex

题解：

如果mex为n，则每次向后插入mex，k次之后不同的值为n+k个
如果mex不为n，则每次插入的都是同一个值，如果这个值出现过，k次之后不同的值为n个；如果没出现过，k次之后不同的值为n+1个

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int t;
long long n,k,a[maxn];
long long getmex(){
	int v=0;
	for(int i=1;i<=n;i++,v++){
		if(v!=a[i])return v;
	}
	return v;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%lld%lld",&n,&k);
		for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
		sort(a+1,a+1+n);
		long long mex=getmex();
		if(mex==n)printf("%lld\n",n+k);
		else{
			if(k==0){
				printf("%lld\n",n);
				continue;
			}
			long long  mid = ceil((mex+a[n])/2.0);
			if(a[lower_bound(a+1,a+n+1,mid)-a]==mid)printf("%lld\n",n);
			else printf("%lld\n",n+1);
		}
	}
	return 0;
}

C . Diamond Miner

题意：

n个矿工在y轴上，n个矿在x轴上，一个人挖一个，花费的力气是点之间的欧几里得距离。问如何分配使得总花费最小

数据范围：

\[\left( 1 \leq n \leq 10^{5}\right)\]

题解：

绝对值相同的点是等价的，直接用|x||y|来代替x,y

会发现两个数组排序后，顺着配的值最小，即小的和小的，大的和大的。

证明方法是排序不等式：

定理：设 \(0<a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n}, 0<b_{1} \leqslant b_{2} \leqslant \cdots\leqslant b_{n}\) 为两组实数, \(c_{1}, c_{2}, \cdots, c_{n}\) 为 \(b_{1}, b_{2}, \cdots, b_{n}\) 的任一排列，则有 \[ \begin{array}{l} \sqrt{a_{1}^{2}+b_{n}^{2}}+\sqrt{a_{2}^{2}+b_{n-1}^{2}}+\cdots+\sqrt{a_{\mathrm{n}}^{2}+b_{1}^{2}} \\ \geqslant \sqrt{a_{1}^{2}+c_{1}^{2}}+\sqrt{a_{2}^{2}+c_{2}^{2}}+\cdots+\sqrt{a_{n}^{2}+c_{n}^{2}} \\ \geqslant \sqrt{a_{1}^{2}+b_{1}^{2}}+\sqrt{a_{2}^{2}+b_{2}^{2}}+\cdots+\sqrt{a_{n}^{2}+b_{n}^{2}} \end{array} \] 其中全相等 \(\Leftrightarrow a_{1}=a_{2}=\cdots=a_{n}\) 或 \(b_{1}=b_{2}=\cdots=b_{n} .\)

证明方法，把两个排列相减呗

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int t, n;
long long a[maxn],b[maxn];
double dis;
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		dis=0;
		int tot=n*2,tot1=0,tot2=0;
		long long x,y;
		for(int i=1;i<=tot;i++){
			scanf("%lld%lld",&x,&y);
			if(x==0)a[++tot1]=abs(y);
			else b[++tot2]=abs(x);
		}
		sort(a+1,a+1+n);
		sort(b+1,b+1+n);
		for(int i=1;i<=n;i++){
			dis+=sqrt(a[i]*a[i]+b[i]*b[i]);
		}
		printf("%.10lf\n",dis);
	}
	return 0;
}

补充下关于 \(\sum_{i=1}^{n} \sqrt{a_{i}^{2}+b_{i}^{2}}\left(a_{i}, b_{i} \in \mathbf{R}\right)\) 的不等式定理

柯西不等式：设 \(a_{1}, a_{2}, \cdots, a_{n} ; b_{1}, b_{2}, \cdots, b_{n}\) 为实数, \(n \in \mathbf{N}\),\(n \geqslant 2,\) 则 \(\sqrt{a_{1}^{2}+b_{1}^{2}}+\sqrt{a_{2}^{2}+b_{2}^{2}}+\cdots+\sqrt{a_{n}^{2}+b_{n}^{2}} \geqslant\) \(\sqrt{\left(a_{1}+a_{2}+\cdots+a_{n}\right)^{2}+\left(b_{1}+b_{2}+\cdots+b_{n}\right)^{2}}\) 其中等号成立 \(\Leftrightarrow\) 存在非负实数 \(\lambda\) 及 \(\mu(\lambda, \mu\) 不同时为0)\(,\) 使得 \(\lambda a_{i}=\mu b_{i}(i=1,2, \cdots, n) .\)

D . Let's Go Hiking

先丢一个队友题解链接：https://blog.csdn.net/weixin_43877657/article/details/114933752

题意：

给出一个长度为n的排列，a先选一个位置，然后b再选一个位置，两人每次都可以向周围移动1位，满足移动后的位置a的值比原来小，b的值比原来小。两人都会采取最优策略，问初始时a选位置能赢的个数

数据范围：

\[\left( 2 \leq n \leq 10^{5}\right)\]

题解：

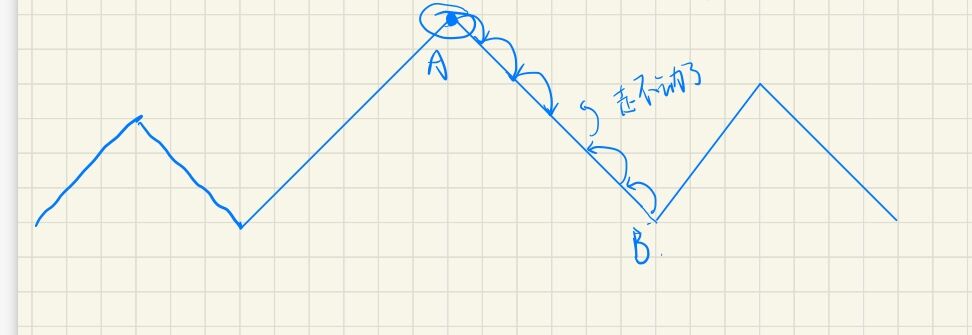
首先a要选在坡顶，坡腰b能把它堵死
a要选在最大峰的坡顶，否则b能选能大峰的坡地开始走
这个破必须长度为奇数，a会与b对着走，奇数才能在相会时让b无法走
不能有其他坡和这个坡长度相同，也就会说这个破不仅最大还唯一，否则b可以走那个

画个示意图，注意上面4点坑

a,b,k=map(int,input().split())
if(k==0):
    s='1'*b+'0'*a
    print("Yes\n"+s+"\n"+s)
elif(a==0):
    print("No");
else:
    if a+b-2<k or b==1:
        print("No")
    else:
        s='1'*(b-1)+'0'*(a-1)
        print("Yes")
        print(s[:a+b-k-1]+'1'+s[a+b-k-1:]+'0')
        print(s[:a+b-k-1]+'0'+s[a+b-k-1:]+'1')

比赛时：

那个破不能超过一个没想到qwq