A. Perfectly Imperfect Array
题解
只要任意一个数不是平方数就可以
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include<bits/stdc++.h>
using namespace std;
int const maxn=2e5+10;
int main(){
int t,n,a,v;
cin>>t;
while(t--){
scanf("%d",&n);
bool flag=false;
for(int i=1;i<=n;i++){
scanf("%d",&a);
v=sqrt(a);
if(v*v!=a)flag=true;
}
if(flag)printf("YES\n");
else printf("NO\n");
}
return 0;
}
|
B . AND 0, Sum Big
题意:
给你N和K, 问有多少长度为n的数组满足:
- 所有元素在[0,\(2^k-1\) ]范围内
- 所有元素AND值为0
- 所有元素之和尽可能大
题解:
快速幂:二进制k位,只要每一位有一个0就能满足条件2,为了满足条件3每一位只能在数组中的一个数中为0,所以每一位的选择有n个数,答案为\(n^k\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #include<bits/stdc++.h>
using namespace std;
long long p=1e9+7;
long long n,k,t;
long long pow_fast(long long a,long long b,long long mod){
long long num=1%mod;
for(;b;b>>=1,a=a*a%mod)
if(b&1)num=num*a%mod;
return num;
}
int main(){
cin>>t;
while(t--){
scanf("%lld%lld",&n,&k);
long long ans=pow_fast(n,k,p);
printf("%lld\n",ans);
}
return 0;
}
|
C . Product 1 Modulo N
题意:
给定n,问[1,n-1]范围内,最多可以取多少数,使其乘积取模n为1
数据范围:
\[\left( 2 \leq n \leq 10^{5}\right)\]
题解:
首先知道一个结论:如果a,b的最大公约数g=gcd(a,b)不为1,则a%b大于1,因为a%b的余数一定是g的倍数。
(1) a%b = (a/g) % (b/g) * g
所以只能选与n互质的数,他们的乘积取余n的结果x也与n互质,x就在刚刚所取的数中,只要把x删掉就行了
证明1: a%b = (a/g) % (b/g) * g

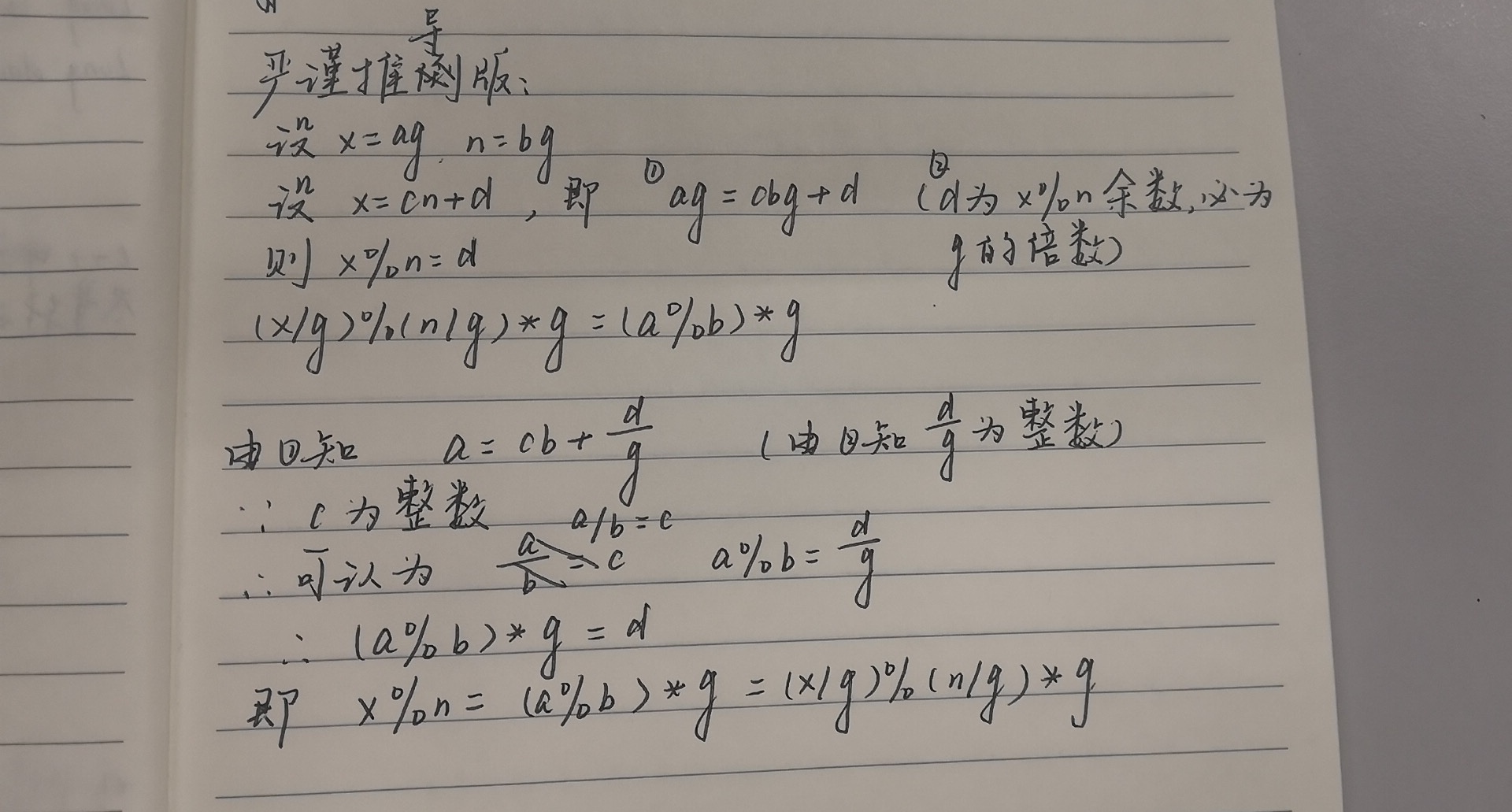
证明:2:与b互质的数乘积取余b的余数与b互质
设 \(a_1,a_2,a_3..a_m\) 与b互质 z=a_1a_2a_3 z=n*b+p g=gcd(n,p) n=cg , p=dg z=gcb+dg=g(cb+d) 则 g是 z 的因子,如果g ≠ 1,则n与 z不互质,与题设矛盾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include<bits/stdc++.h>
using namespace std;
vector<int> v;
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int main(){
int n;
scanf("%d",&n);
v.push_back(1);
long long tmp=1;
for (long long i=2;i<n;i++){
if (gcd(i,n)==1){
v.push_back(i);
tmp=(1ll*tmp*i)%n;
}
}
if (tmp==1ll) cout<<v.size()<<endl;
else cout<<v.size()-1<<endl;
for (long long i=0;i<v.size();i++){
if (v[i]==tmp&&tmp!=1) continue;
cout<<v[i]<<" ";
}
cout<<endl;
}
|
网上看到的另一种不错证明,原文链接
不能选与n不互质的数, 因为选了之后%n一定不为1,因为gcd(乘积,n)!=1. 证明: 设gcd(p,n)=z,则p=xz,n=yz, 设选的其他数乘积为q, 则pq%n=1,设pq=kn+1, 那么qxz=kyz+1, (qx-ky)z=1, 当且仅当z=1时式子才有可能成立, 而gcd=z>1,因此式子不可能成立, 所以如果选择了gcd!=1的数,一定不满足条件.
因此只能选与n互质的数, 设s为所有与n互质的数的积对n取模的结果, 如果s=1,那么这些数全部可以选择, 如果s!=1,此时s一定与n互质,因此s也在这些数中, 那么选除了s的其他数就行了
D. Cut and Stick
题意:
给出长度为n的序列a,q个询问,每次询问[l,r]区间。
问至少把区间内的数重新组合成几段,才能满足每段众数的次数不超过 \(\left \lceil len \right \rceil\) , len为区间长度
数据范围:
\(\left( 1 \leq n,q \leq 3*10^{5}\right)\)
\(a_{1}, a_{2, \ldots,} a_{n}\left(1 \leq a_{i} \leq n\right)\)
\((1 \leq l \leq r \leq n)\)
题解:
- 如果初始区间众数个数< \(\left \lceil len \right \rceil\) , 则不用拆,答案为1。否则就要拆,关于每段如何拆分。
偶→奇+奇 ,可容纳数增加1;奇→偶+奇,可容纳数不变。于是每次就是尽量拆偶数,变化如下
初始偶→奇+奇→偶+奇+奇→奇+奇+奇+奇→偶+奇++奇+奇+奇...
初始奇→偶+奇→奇+奇+奇→偶+奇++奇+奇...
实际上就是初始为偶数多了一步,后面跟奇数一样拆法。每多1个,段数+2。
- 莫队求区间众数,时间复杂度n*sqrt(n)。开一个数组num记录每个数的个数,数组cou[x]记录数量为x的数有几个。
每次区间增加时,增加这个数的个数,维护cou。还有判断增加后是否变成区间众数
区间变小时,减少这个数的个数,维护cou。看当前众数个数值的cou是否变为0,如果变为0说明当前数为唯一众数,众数个数应该-1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
using namespace std;
//
int const MAXN = 3e5+7;
int a[MAXN],unit,n,m,nowmax,cnt[MAXN],ans[MAXN],num[MAXN];
struct query1{
int L,R,id;
}qu[MAXN];
bool cmp(query1 a,query1 b){
if(a.L/unit == b.L/unit) //相同块,对R排序
return a.R < b.R;
else return a.L/unit <b.L/unit; //不同块,对块排序
}
void mo_add(int x){
cnt[num[a[x]]]--;
num[a[x]]++;
cnt[num[a[x]]]++;
if(num[a[x]]>nowmax)nowmax=num[a[x]];
}
void mo_del(int x){
cnt[num[a[x]]]--;
num[a[x]]--;
cnt[num[a[x]]]++;
if(cnt[nowmax]==0)nowmax--;
}
void work(){
int L = 1,R = 0;
for(int i=0;i<m;i++){
while(R < qu[i].R){
R++;
mo_add(R);
}
while(R > qu[i].R){
mo_del(R);
R--;
}
while(L < qu[i].L){
mo_del(L);
L++;
}
while(L > qu[i].L){
L--;
mo_add(L);
}
// debug(nowmax,1);
if(nowmax<=ceil((R-L+1)/2.0))ans[qu[i].id]=1;
else{//奇偶不同拆法
int z=1,len=R-L+1,u=nowmax-ceil((R-L+1)/2.0);
if(len%2==0){z++;u--;}
while(u){
z+=2;u--;
}
ans[qu[i].id]=z;
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
unit=sqrt(n);
for(int i=0;i<m;i++){ //读入查询
scanf("%d%d",&qu[i].L,&qu[i].R);
qu[i].id = i;
}
sort(qu,qu+m,cmp);
work();
for(int i=0;i<m;i++){
printf("%d\n",ans[i]);
}
return 0;
}
|
比赛时:
想到了莫队,但是当莫队区间变小时卡住了,忘记了只要再维护一个众数的个数有多少就行了。